阅读本篇题解之前,请先完成Luogu P3372。
题目描述
如题,已知一个数列,你需要进行下面三种操作:
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:
输出包含若干行整数,即为所有操作3的结果。
输入输出样例
输入样例#1:
1 | 5 5 38 |
输出样例#1:
1 | 17 |
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^)
样例说明: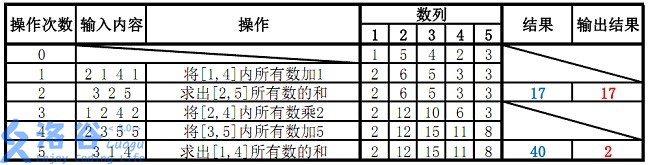
故输出应为17、2(40 mod 38=2)
对比P3372,本题的提升在于,多了对乘法的要求(大家都看见了啊喂)。
不过,这一看起来小小的要求,真的要实现的时候,才发现真的难写。果然加了这一条就从P3372的绿题变成蓝题了。
在P3372中,区间修改仅要求了加法,因而每次下放lazy标记的时候只需要暴力下放,也就是ans[p]+和tag[p]+。然鹅,在本题中因为多了乘法,lazy标记在下放时就出现了一个问题:先下放加法lazy标记(addtag)还是乘法lazy标记(multag)?
答案就是先下放multag,再下放addtag。
为什么呢?因为在四则运算中,加法优先级较低,乘法较高,故乘法会影响加法,在下放multag的时候不仅要ans[p]+,还要addtag[p]+,还要multag[p]+(三个p均为同一子结点)。这样,之后在下放addtag的时候才能加出正常数值。
还有就是,时刻注意取模。
附代码:
1 |
|